Como já especificamos em diversos textos deste site, a medicina pode parecer muitas vezes uma ciência subjetiva e incerta, porém existem meios de torná-la mais objetiva e direta na busca correta do diagnóstico e nas demais condutas.

Uma das maneiras para isso é o uso racional dos exames complementares. Aprender quando solicitar e como interpretar testes diagnósticos pode ajudar a melhorar bastante a segurança dos pacientes.

Nesse sentido, em um texto passado falamos sobre a sensibilidade e especificidade dos testes diagnósticos. Percebemos que essas características dos testes diagnósticos são importantes na busca pelo diagnóstico correto.

Contudo, não são dados que ajudam diretamente para determinar o grau de auxílio que um exame pode trazer para descartar ou para confirmar o diagnóstico de uma doença investigada em um paciente individual.

Assim, prometemos simplificar a vida de vocês trazendo um conceito mais útil e diretamente aplicável na prática clínica: a Likelihood Ratio (LR). Certamente, esta é a característica clinicamente mais importante dos testes diagnósticos!

Neste texto, vamos explicar o passo-a-passo para utilizá-la, tentando descomplicar ao máximo a matemática envolvida.

O que é a LIKELIHOOD RATIO?

Likelihood Ratio: é probabilidade de um achado (exame físico, diagnóstico) estar presente em um paciente com a doença investigada, em comparação com um paciente sem essa doença.

Quando o valor da LR é acima de 1, a presença daquele achado aumenta as chances de a doença estar presente. Já valores abaixo de 1, a possibilidade de a doença estar presente diminui.

Existem dois tipos de LR:

  • LR positiva (LR +): seu valor indica o quanto o teste AUMENTA a chance de doença se o teste resultar positivo.
  • LR negativa (LR -): seu valor indica o quanto o teste DIMINUI a chance de doença se o teste resultar negativo.

Como calcular a likelihood ratio?

LR + : a probabilidade de uma pessoa DOENTE ter um teste POSITIVO divido pela probabilidade de uma pessoa SADIA ter um teste POSITIVO.

Fórmula: Verdadeiros positivos em doentes ÷ falsos positivos em sadios = Sensibilidade ÷ 1- Especificidade.

LR – : a probabilidade de uma pessoa DOENTE ter um teste NEGATIVO dividida pela probabilidade de uma pessoa SADIA ter um teste NEGATIVO.

Fórmula:  Falsos negativos em doentes ÷ verdadeiros negativos em sadios = 1- Sensibilidade ÷ Especificidade.

Assim, basta possuir os valores de Sensibilidade e de Especificidade do teste em questão para calcular a LR + e a LR- .

Para facilitar nossa vida, existem calculadoras online, como a http://getthediagnosis.org/calculator.htm

Exemplo: no texto anterior avaliamos a sensibilidade e a especificidade do teste rápido para COVID-19, respectivamente 86% e 99%. Fazendo os cálculos ou utilizando a calculadora online, determinamos a LR+ = 86 e LR- = 0,14.

Como utilizar a LIKELIHOOD RATIO?

A LR é um valor que pode ser multiplicado diretamente pela CHANCE PRÉ-TESTE da doença para obter a CHANCE PÓS-TESTE da doença.

OBS.: Ambas os tipos LR são utilizadas da mesma maneira.

Beleza, não parece tão difícil. Mas o que é essa tal de probabilidade pré-teste?

Probabilidade pré-teste: é a probabilidade de o paciente possuir determinada doença antes de se aplicar um achado clínico ou um resultado de teste diagnóstico.

como estimar a probabilidade pré-teste?

Bem, mas como podemos determinar isso?

Devemos lembrar que os dados da história clínica e do exame físico correspondem a grande parte do necessário para se alcançar o diagnóstico completo, sendo a coleta dos dados um dos três pilares do diagnóstico.

A partir da apresentação inicial do paciente já podemos pensar em possíveis doenças que se encaixam na manifestação clínica. Diante dela, possuímos algumas maneiras de transformar essas ideias de diagnóstico em probabilidades (porcentagens):

  • A Prevalência de uma patologia dentro daquela população. Por exemplo, um homem de 82 anos com “esquecimento” entra em seu consultório ou no PS do hospital. Qual a probabilidade pré-teste de DEMÊNCIA? Segundo estudos epidemiológicos, a prevalência de demência nessa faixa etária é de 16%.

É uma maneira de se determinar, mas possui algumas limitações, como a necessidade de pesquisar esses dados na literatura ou em artigos mais recentes, além de não levar em consideração nenhuma característica específica e individual do paciente em questão, haja vista ser apenas uma média da população.

  • A Frequência da doença em pessoas com aquele quadro clínico. Também existem estudos que estimam a probabilidade de o indivíduo ter aquela doença de acordo com alguns sinais e sintomas.

Por exemplo em um homem com déficit neurológico agudo, não comatoso e sem trauma crânio encefálico, a frequência de AVE entre essas pessoas é de 10%.

Novamente, a limitação está relacionada a não levar em consideração muitas outras características desse indivíduo.

  • Escores de Risco: fórmulas comprovadas por estudos e aprovadas por sociedades de especialistas, que levam em consideração vários sinais e sintomas, bem como características dos indivíduos (sexo, idade, estilo de vida, vícios) para determinar a probabilidade pré-teste daquele indivíduo possuir a doença investigada.

Um exemplo é o CAD consortium, um Escore utilizado para determinar a probabilidade do paciente estar sofrendo uma doença arterial coronariana, o qual leva em consideração idade, sexo, tipo de dor torácica (Anginosa típica, atípica ou inespecífica), presença diabetes, hipertensão e dislipidemia, histórico de fumante, além do escore de Cálcio coronariano (?). Para um homem, 50 anos, com dor anginosa atípica, sem comorbidades e fumante, a sua probabilidade pré-teste de sofrer uma DAC é de apenas 12%.

A grande vantagem desse método é sua larga disponibilidade em aplicativos de celular, que fazem um compilado dos Escores mais utilizados. Um muito bacana é o Qx Calculate.

  • Talvez dentre todas, a mais utilizada seja o Palpite do médico, baseado em suas experiências prévias, no seu “feeling”. Muitas vezes é difícil determinar uma porcentagem, mas realizam classificações simples como: esses achados clínicos indicam que essa doença é MUITO provável / MODERADAMENTE provável / POUCO provável de ocorrer.

Quer testar sua intuição? Vamos a um exemplo: um homem, idoso, fumante, com dispneia progressiva a 6 meses, associado a tosse produtiva sanguinolenta (?) e perda de peso recente. Como você classificaria esse paciente para CA de pulmão? Você deve ter pensado em “MUITO provável”, e certamente realizaria o protocolo adequado para o diagnóstico de CA pulmonar.

Agora que você já entendeu como determinar a probabilidade pré-teste, vamos aprender a usar a Likelihood Ratio, para chegarmos mais próximo do diagnóstico correto.

Primeiramente, devemos entender como a LR ajuda na pesquisa da doença correta, mediante os dados da história clínica e os exames adequados. A partir do momento que determinamos uma probabilidade pré-teste segura, delimitamos melhor os possíveis diagnósticos que aquele paciente possui. Diante disso, ao aplicarmos a LR+ podemos aumentar a chance da doença; no caso da LR-, diminuir a chance.

Ao unir a LR com a probabilidade pré-teste previamente determinada, chegamos na probabilidade pós-teste, isto é, a nova chance de o indivíduo estar sofrendo da doença pesquisada.

Mas precisa usar matemática?

Para isso, existem diversos cálculos matemáticos e transformações necessárias para chegar no resultado precisamente. Contudo, temos maneiras práticas e rápidas de unir LR com a probabilidade pré-teste.

A primeira delas é o Nomograma de Fagan. Esse método consiste em um gráfico com 3 colunas. A primeira da esquerda é a coluna da probabilidade pré-teste, a localizada no meio é o valor da LR (positiva ou negativa) e a da direita é a probabilidade pós-teste. Como utilizá-lo? Simples, basta traçar uma linha entre os valores já conhecidos da primeira e da segunda coluna, continuando até o valor correspondente estimado da probabilidade pós teste.

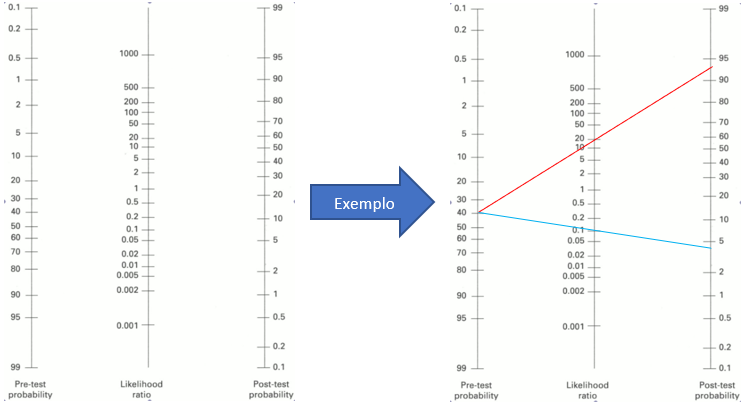
Exemplo: Um paciente com probabilidade pré-teste de 40% realiza um teste com LR + = 20, qual sua probabilidade pós-teste? Entre 90-95% (Linha vermelha).

E se fosse com a LR – de 0,1? A probabilidade pós-teste seria entre 2-5% (Linha Azul-claro).

Uma maneira ainda mais simples foi desenvolvida pelo Dr. Steven McGee, bastando utilizar uma tabela e uma adição simples. Esse médico percebeu que existia uma relação entre o valor da LR e a mudança aproximada na probabilidade (da pré-teste para a pós-teste). Assim, com a LR em mãos, basta verificar o quando se deve somar ou subtrair da probabilidade pré-teste para alcançar o resultado da probabilidade pós-teste.

Exemplo: um paciente com 30% de probabilidade pré-teste para obstrução intestinal, apresenta abdome distendido (LR+ = 9.6). Qual sua probabilidade pós-teste? Segundo a tabela, LR de 9.6 indica aumento aproximado de 45% na probabilidade. Assim, soma 30% (pré-teste) com 45% (achado clínico), o resultado é de 75%.

A partir dessa tabela podemos classificar os testes (achados) diagnósticos de acordo com o grau de ajuda deles em confirmar ou descartar os diagnósticos prováveis.

Dessa maneira, percebemos dois fatos importantes. O primeiro é que exames fortes, isto é, aqueles que podem te fazer saltar de uma baixa probabilidade pré-teste, para uma probabilidade pós-teste elevada (e vice-versa), são aqueles que possuem LR + >10 ou   LR – < 0,1. Assim, devemos nos informar e ter em mente quais os exames e sinais que mais alertam uma doença, ou que sua ausência a descarta.

O segundo fato é a independência dos valores de LR + e LR – dentro de um mesmo exame. Assim, não significa que se um exame é forte para confirmar a doença, ele também será capaz de descarta-la. Um bom exemplo é supradesnivelamento de segmento ST no eletrocardiograma para diagnóstico de infarto agudo de miocárdio (IAM). Ele possui uma LR+ de 22.3, logo, caso o sinal esteja presente, a probabilidade daquele paciente estar sofrendo IAM aumenta mais de 45%, sendo um exame forte para confirmação. Contudo, sua LR- é 0,6 , ou seja, sua ausência apenas reduz em 15% a probabilidade de IAM, sendo um exame fraco para negar o diagnóstico.

ONDE ENCONTRAR OS VALORES DE LR?

Bem se é tão importante e útil a Likelihood Ratio devemos estar constantemente pesquisando e guardando algumas, talvez as mais utilizadas no dia a dia da sua especialidade.

Os próprios livros-texto, revisões, bem como Guidelines e diretrizes fornecem os valores de LR. Ou pelo menos concedem os valores de sensibilidade e especificidade, e agora sabemos como calcular a LR a partir deles.

Também existem site especializados no assunto como:

DocLogica
Getthediagnosis
TheNNT

Além disso, existem dois livros excelentes que fazem um compilado de artigos sobre medicina baseado em evidências, que no final de vários capítulos existe um resumo dos principais achados clínicos e exames com suas respectivas LR.  São eles:

CONCLUSÕES:

Percebemos como fica muito mais fácil utilizar os conceitos de LR e de probabilidade pré-teste no dia a dia da prática clínica, em vez de muitas vezes ficar confusos quando ao uso correto da sensibilidade e da especificidade.

Assim, embora todas as características dos testes diagnósticos (e também dos achados clínicos) sejam importantes, com cada uma possuindo uma função, a LR provou ser a mais prática, objetiva e útil para medir o grau de ajuda que um exame ou um sinal pode oferecer em busca do diagnóstico correto.

O próximo passo é se acostumar com esse conceito, incorporando em sua prática clínica, e espalhar para mais pessoas! Quem sabe isso não resolva muitos casos clínicos difíceis ou poupe tempo e dinheiro, não pedindo mais exames desnecessários ou inúteis para certas doenças.

Quer um resumo sobre esse assunto, para carregar por onde você for? Logo abaixo haverá o botão para a página para fazer o download!

 

PARA SABER MAIS:

MCGEE, Steven R. Evidence-based physical diagnosis. 4ed. Philadelphia, PA: Elsevier, 2018.

SIMEL, David L.; RENNIE, Drummond; KEITZ, Sheri A. The Rational Clinical Examination: Evidence-Based Clinical Diagnosis. United States of America: American Medical Association, 2009.

Esquema ilustrado

Autor:

Alexandre Wilton Bissoli Júnior

Você pode referenciar o artigo acima usando o Digital Object Identifier (Identificador de Objeto Digital) – DOI.

DOI: 10.29327/823500-99